射影幾何に基づく多視点カメラの中間視点映像生成

斎藤 英雄, 木村 誠, 矢口 悟志, 稲本 奈穂, "射影幾何に基づく多視点カメラの中間視点映像生成", Vol.43, No.SIG 11(CVIM 5), pp.21-32, 2002.

1. 目的

多視点カメラを用いて撮影した対象空間を任意視点から観察可能なシステムの開発．

2. 提案手法

2.1 射影グリッド空間での 3 次元復元に基づく中間視点画像生成

本論文では，多視点カメラシステムにおいて，強校正を使わずに弱校正のみを行うことにより得られるカメラ間の射影的関係を表す基礎行列（F 行列）を利用し，多視点画像に撮影された対象空間の 3 次元的幾何情報を射影的に推定することによって，多視点画像間の画素ごとに対応関係を求め，この対応関係を用いて，実カメラ視点の中間の視点における画像を生成するための以下の2 つの手法について述べている．

2.1.1 射影グリッド空間における 3 次元形状復元

弱校正された多数のカメラの中から選択された 2 台の基底カメラを用いて対象空間に射影グリッド空間と名付けられたグリッド座標を設定し，射影グリッド空間内で対象の 3 次元形状を視体積交差法を利用して復元する．

2.1.2 中間視点画像生成

つぎに，復元された 3 次元モデルから中間視点画像を生成する．この 3 次元モデルは，射影変換の曖昧性を含んだ 3 次元形状であり，真の形状を表していないが，実カメラ画像間の画素ごとの対応関係や 3 次元モデル上の各点の実カメラに対する前後関係・射影関係は求めることができる．そこで，射影グリッド空間において復元された 3 次元モデルの各点が，実カメラに見えるのかどうかの可視判定を行い，その関係から，入力画像間の画素ごとの対応関係が与えられれば，モーフィング手法 *1を視点内挿 *2に利用することにより，入力画像間の中間視点画像を生成することができる．下図に，対象空間を取り囲むように配置された 18 台のカメラを用いて撮影された多視点画像列のあるフレームについて，提案手法により中間視点画像を生成した例を示す．この図の 3 角形の頂点が合成を用いた実カメラ画像である．

2.1.3 複数対象空間の統合 

サッカーフィールド等のように広大な空間を対象空間とするとき，個々のカメラがフィールド全域をとらえていると，フィールドに存在する選手等が画面に占める割合が相対的に小さくなってしまい，選手等の物体に対する画像の解像度が不足することになる．そこで，対象空間を複数の小空間（セル）に分割し，セルごとに 3 次元モデルを構築し，統合することによって全体の 3 次元モデルを構築し，中間視点画像を生成する．ここでは，対象空間全体が画角に収まるような 2 台のカメラを基底カメラとして，複数のセルに共通の射影グリッド空間の座標系を設定する．したがって，基底カメラが共通であれば，射影グリッド空間内の 3 次元モデルはすべてのカメラ画像に投影することができることから，複数のセルで作成した 3 次元モデルを統合し，前述の中間視点画像生成の枠組みを用いることができる．

2.2 サッカー映像の中間視点映像生成 

本手法では，サッカースタジアムの観客席等の適当な位置に固定した数台のカメラで撮影した映像を入力とする．まず始めに，入力映像から適当なフレームを選び，そこから自然特徴点を手入力により抽出することにより F 行列を算出する．しかし，射影グリッド空間を設定したとしても，対象空間を全周囲から取り囲むようなカメラ配置で撮影されていなければ視体積交差法を適用した 3 次元形状復元は困難である．ここでは，対象空間を全周囲から取り囲まない多視点画像からでも，隣接するカメラ間の射影幾何学的関係を利用して中間視点画像を生成する手法について述べる．本手法では，移動領域（選手とボール）と，それら以外の静止領域に分け，領域ごとに隣接するカメラ間で画素ごとに対応点を決定し，2.1.2 節と同様に中間視点画像を生成し，最後にこれらの領域を合成する．

2.2.1 静止領域

対象空間がサッカースタジアムであることを利用して，いくつかの平面領域に分割できるものと近似する．平面に近似された各領域に対して，隣接するカメラ間の平面射影行列（Homography）を用いて画素ごとに対応点を決定し，中間視点画像を生成する．この平面射影行列は，対応する領域内で数点の対応点を手入力により検出することにより算出する．

2.2.2 移動領域

入力された多視点映像から，背景差分によって移動領域（選手とボール）を検出する．そして，検出された移動領域をカメラ間での対応付けを行う．この対応付けには，選手の足元がグラウンドに接しているという前提を利用して，領域の最下部の点の座標が，グラウンド面の平面射影行列により関連付けられることを用いる．つぎに，隣接するカメラ間で対応付けられた移動領域内部について，密な対応点関係を求める．移動領域の上部から下部にかけてエピポーラ線を順に投影していき，隣接するカメラ間の各エピポーラ線と移動領域の両端との交点に対し対応付けを行う．そして，この対応関係を用いて中間視点画像を生成する．

3. まとめ

本論文では，実カメラ視点の中間の視点における画像を生成するための 2 つの手法について述べられている．一つは，射影グリッド空間において，視体積交差法を用いて対象空間の 3 次元復元を行い，復元された 3 次元モデルから実カメラ視点の中間視点画像を生成する方法を示している．もう一つは，視体積交差法を利用した 3 次元復元が困難となるシーンを撮影した多視点画像を用いた中間視点画像生成を行うために，移動領域と静止領域を分割し，それぞれの射影幾何学的性質に基づいて中間視点画像を生成し，それらを合成する手法を示している．

本論文では，中間視点画像の仮想視点が，2 ないし 3 つの参照画像の視点を指定した重みで内分した位置になると仮定している．しかし，参照画像を撮影したカメラの位置関係によっては，中間視点画像の見え方に大きな歪みを発生させる可能性がある．また，本論文では，視点の内挿に 2 台か 3 台のカメラを用いる手法について述べた．この場合，内挿した中間視点が移動できる範囲は限定される．

 

4. 用語説明

・強校正

対象空間のユークリッド座標系とカメラ座標系の射影関係の推定による校正のこと．強校正を行うには，空間上の数点に対し，ワールド座標系における 3 次元座標と画像座標系における 2 次元座標を正確に測定し計算する方法が一般的である．

・弱校正

カメラ間の射影幾何学的関係の推定による校正のこと．各カメラに共通して見えるマーカ点から検出したカメラ間の対応関係から，カメラ間の射影幾何学的関係を F 行列として得られる．この F 行列の推定に利用する対応関係は，3 次元点の未知ないくつかの自然特徴点を検出することによって得られるため，強校正に必要な3 次元座標の既知な人工的マーカを対象空間に配置する必要がなく，労力を格段に削減することができる．

・射影グリッド空間

数台あるカメラシステムのうちの任意の 2 台を基底カメラ 1，2 とする．下図に示すように，この 2 台のカメラそれぞれの視点からの中心射影によって 3 次元空間を定義する．つまり，空間を定義する 3 軸として，基底カメラ 1 の画像の X 軸，Y 軸，そして基底カメラ 2 の画像の X 軸を用いるわけである．そして，これらの 3 軸を各 P，Q，R 軸として，射影グリッド空間を定める．

これによって，下図（A）のようにカメラ配置とは無関係にユークリッド座標系を考えるのではなく，下図（B）のように任意に配置された多視点カメラ間の関係を示す F 行列によって，各カメラと対象の 3 次元空間を関連付けることができる．

・視体積交差法

各視点の画像から対象物体のシルエットを抽出し，このシルエットにより決定される視体積を共通の 3 次元空間で交差させ，その共通部分である Visual Hull *3を対象形状として復元するものである．この手法は対象空間を全周囲から取り囲むようなカメラ配置で撮影されている必要がある．

*1:T. Beier, S. Neely, "Feature-Based Image Metamorphosis", Proc. SIGGRAPH'92, pp.35-42, 1992.

*2:S. Chen, L. Williams, "View Interpolation for Image Synthesis", Proc. SIGGRAPH'93, pp.279-288, 1993.

*3:A. Laurentini, "The Visual Hull Concept for Silhouette Based Image Understanding", IEEE Trans. Pattern Analysis and Machine Intelligence, Vol.16, No.2, pp.150-162, 1994.

多視点画像からの自由視点映像生成技術の動向

H. Saito, "Recent Advance of Free-view Movie Generation from Multiple View Images", IEEJ Transactions on Electoronics, Information and Systems, Vol.121, No.10, pp.1493-1499, 2001.

1. カメラ切り替えによる映像効果

　EyeVision では， 30 台のカメラがフットボールフィールドを取り囲むように取り付けられた．そして，これらのカメラで同時に撮影された映像から，カメラを連続的に切り替えることにより，あたかもカメラがフットボールフィールドを動き回っているかのような映像効果を実現した．ここで重要だったのは全カメラのパン・チルト動作の同期コントロールである．任意の 1 台をマスターカメラとして，そのカメラを用いて対象の選手が中央に撮影されるようにコントロールすると，残りのカメラはマスターカメラに同期して動く．原理的には，マスターカメラの向きにより定まる直線と選手が存在する平面との交点から選手の大よその 3 次元位置が決定されることを利用して，常に全てのカメラが選手を中央に捕らえているようにコントロールするわけである．

2. 自由視点映像の生成によるカメラの仮想移動

2.1. 対象の 3 次元モデリング

　CMU（Carnegie Mellon University）では，マルチベースラインステレオ法によるステレオ視差復元を多数のカメラに拡張して，対象の全周囲からの 3 次元復元を行い，カメラを仮想的に自由に動かした映像を生成する手法を提案し，この考え方を仮想化現実（Virtualized Reality）と名づけた． CMU で開発された “3D Room” *1は，動きのあるイベントの 3 次元情報をコンピュータ内にデジタル化して取り込むためのシステムである．

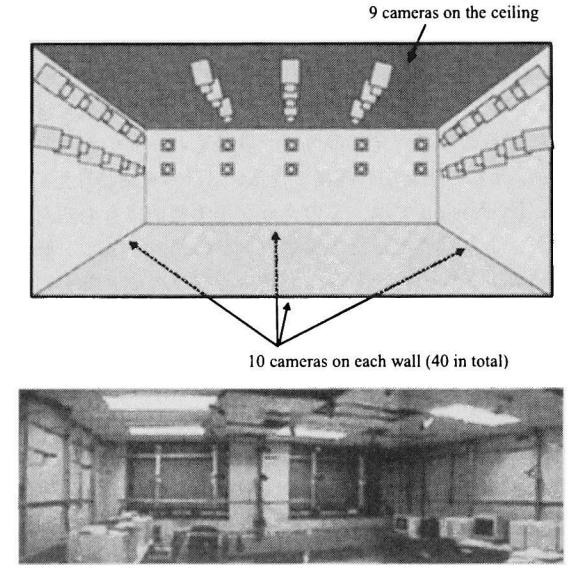
上図の 3D Room により撮影された多視点動画像列から対象の 3 次元構造を再構築するために CMU が採用した手法は，マルチベースラインステレオ法 *2を用いて各カメラ毎に求めた距離画像を体積空間で融合し，3 次元モデルを構築する手法を用いるというものである．

2.2. レンダリング

　構築された 3 次元モデルを用いて，任意視点の画像をレンダリングする手法には以下に述べる 2 つのアプローチが考えられる．一つは，再構築された3次元モデルの各三角メッシュ上に画像からテクスチャを割り当て，任意視点からテクスチャマッピングによりレンダリングする手法（モデルベースド法）*3である．もう一つは，合成しようとする視点付近の 2 枚，もしくは 3 枚の入力画像を選び，これらの入力画像間の対応関係を復元された3次元モデルから求め，この対応関係にもとづいて見かけ上の中間画像を合成する手法（アピアランスベースド法）*4である．

　前者では，三角メッシュを各画像面に投影し，投影された三角領域内のテクスチャを三角メッシュのテクスチャとして割り当てる．このとき，同じ三角メッシュを見るカメラは複数あるため，複数のカメラ間でテクスチャを平均する．この手法の場合，推定した 3 次元モデルに誤差があると，複数のカメラに投影された三角領域のテクスチャに位置ずれが生じる．このため，入力画像を撮影したカメラと同じ位置で任意視点の合成を行ったとしても，画質が劣るという問題がある．

　一方，後者の手法では，まず再構築した 3 次元モデルから画像間の対応点を下図のようにして求める．ここで，対応点を持つ各点について，視差ベクトルが，例えば点 については， から への のように定義できる．この視差ベクトルがオクルージョンにより片方の画像には投影されるがもう一方には投影されないといった場合については，擬似的な視差ベクトルとして定義することにする．このような対応関係を，疑似対応（pseudo correspondence）と呼ぶ．一方，両者の画像に投影され視差ベクトルが定義できるものについては，無矛盾対応（consistent occlusion）と呼ぶ．このような視差ベクトルを用いれば，視差ベクトル上の中間の位置に画素値をマッピングすることにより，画像間の中間の視点の画像（部分中間画像）を合成できる．そして，各画像について合成された画像をさらに合成して，中間画像を生成する．また，この際には，任意視点は選択したカメラ間の合成比率（重み）として与えるため，入力画像と同じ視点の画像を合成しようとする場合は，同じ視点の入力画像の重みが 1 となり，それ以外は 0 となることから，合成される画像は入力画像と全く同じ画質のものが得られる．下図に，同一時刻において 2 つのカメラにより撮影された入力画像より生成した中間画像の例を示す．

2.3. その他のモデリング・レンダリング手法

前節に紹介したアピアランスベースド法は，広くは，イメージベースドレンダリング（IBR）と呼ばれる手法に相当する．この手法は，明示的な 3 次元復元を行わずに画像に基づき任意視点画像を合成しようという，近年注目されている手法である．この IBR による新しい画像合成の関連研究では，Katayama et. al. が，視点を密に変化させて得られる画像列から，任意の視点の画像が合成できることを示した *5．Levoy and Hanrahan *6と Gortler et al. *7は，このコンセプトを拡張し，3 次元空間における任意の光線を表す直線が 4 つのパラメータで表されることに着目し，視点の異なる大量の入力画像から 4 次元の光線空間を構築し，この光線空間において任意視点の各画素に対応する光線の色を推定するという新しい枠組みを提案した．このような手法の問題点は，視点の異なる画像を非常に多く必要とすることであるため，動きのあるイベントに適用することは，非常に多くのカメラを必要としてしまうため適用が困難となることである．

　さて，入力された視点の異なる画像から任意視点画像を合成するための手法として，view interpolation *8 *9と呼ばれる任意視点画像合成法がある．この手法は，複数の入力画像間の対応関係からその中間の画像を補間により合成するものである．view morphing *10は，image morphing *11の拡張であり，ここでは，カメラ間の幾何学的位置関係を正確に扱うことができるようなアルゴリズムが提案されている．先に紹介したアピアランスベースド法による任意視点画像生成法も，この画像の対応関係に基づくものであるが，画像間の対応関係を，多視点画像から再構築した 3 次元モデルから与えることにより画像生成の自動化を実現している．

2.4. 多視点画像のカメラキャリブレーション

多数のカメラを利用して 3 次元復元を行おうとする場合，各カメラのカメラキャリブレーションの精度が，3 次元復元の精度に大きく影響する．このカメラキャリブレーション法として広く利用されているのが，Tsai により提案されたカメラモデルとキャリブレーション法 *12である．この手法により，6 自由度のカメラ外部パラメータと，焦点距離，画素のアスペクト比，光軸の画像平面上の 2 次元座標，そしてレンズのラディアル歪の第一次パラメータの合計 5 つのカメラ内部パラメータを推定する．この推定には，あらかじめ対象空間内に 3 次元位置既知の点を複数与え，これがカメラに投影される位置を検出する必要がある．

　多数カメラのシステムにおいては，複数のカメラ間で共通に見える点を検出して，三角測量の原理により 3 次元構造を復元するものであるため，カメラ間の相対的幾何学関係であるエピポーラ幾何をできるだけ正確に扱うことが重要となる．また一方で，多数のカメラに対して同時に 3 次元位置の既知なマーカを撮影させてキャリブレーションする手間も大きな問題であった．そこで，Saito et. al. は，カメラ間の相対的幾何学的関係を明示的に表現し，かつ 3 次元位置の未知な幾つかの特徴点の対応関係情報のみから推定できるエピポーラ幾何に基づいて多数カメラから 3 次元復元を行う手法として，この多数のカメラ間のエピポーラ幾何から“射影グリッド空間”を構成し，この射影グリッド空間において 3 次元復元する枠組を提案した *13 *14．一般に，カメラ毎に 3 次元空間とカメラの画像座標とを関連づけるための射影変換行列をカメラ毎に推定する必要がある．これに対し，Saito et. al. の提案した“射影グリッド空間”では，このグリッド空間と画像乗の点との関係を，カメラ間のエピポーラ幾何を表す Fundamental 行列（F行列）のみを用いて記述することができるため，カメラ毎に 3 次元空間との射影変換行列を復元することなしに，多数のカメラからの 3 次元復元を行うことが可能になる．この手法を利用することにより，カメラの位置関係が未知，つまりカメラキャリブレーションが行われていない多視点画像に対して，10 点程度の 3 次元位置の未知な特徴点の対応関係から F 行列を求め，この F 行列から射影グリッド空間を構成し，対象物体の 3 次元復元を行うことが可能となる．

*1:T. Kanade, H. Saito, S. Vedula, "The 3D Room: Digitizing Time-Varying 3D Events by Synchronized Multiple Video Streams", CMU-RI-TR-98-34, 1998.

*2:M. Okutomi, T. Kanade, "A Multiple-Baseline Stereo", IEEE Trans. on PATTERN ANALYSIS AND MACHINE INTELLIGENCE, Vol.15, No.4, pp.353-363, 1993.

*3:S. Vedula, P. W. Rander, H. Saito, T. Kanade, "Modeling, Combining, and Rendering Dynamic Real-World Events From Image Sequences", Proc. 4th Conf. Virtual Systems and Multimedia, Vol.1, pp.326-322, 1998.

*4:H. Saito, S. Baba, M. Kimura, S. Vedula, T.Kanade, "Apperance - Baced Virtual View Generation of Temporally-Varying Events from Multi-Camera Images in 3D Room", Second International Conference on 3-D Digital Imaging and Modeling (3DIM99), October 4-8, pp.516-525, 1999.

*5:A. Katayama, K. Tanaka, T. Oshino, H. Tamura, "A view point dependent stereoscopic display using interpolation of multi-viewpoint images", SPIE Proc. Vol.2409, Stereo scopic Displays and Virtual Reality Systems II, pp.11-20, 1995.

*6:M. Levoy, P. Hanrahan, "Light Field Rendering", Proc.SIGGRAPH'96, 1996.

*7:S. J. Gortler, R. Grzeszczuk, R. Szeliski, M. F. Cohen, "The Lumigraph", Proc. SIGGRAPH '96, 1996.

*8:S. Chen, L. Williams, "View Interpolation for Image Synthesis",Proc. SIGGRAPH'93, pp.279-288, 1993.

*9:T. Werner, R. D. Hersch, V. Hlavac, "Rendering RealWorld Objects Using View Interpolation", In IEEE Int'l Conference on Computer Vision: ICCV95, pp.957-962, 1995.

*10:S. M. Seitz, C. R. Dyer, "View Morphing", Proc.SIGGRAPH '96, pp.21-30, 1996.

*11:T. Beier, S. Neely, "Feature-Based Image Metamorphosis", Proc. SIGGRAPH '92, pp.35-42, 1992.

*12:R. Tsai, "A Versatile Camera Caribration Technique for High- Accuracy 3D Machine Vision Metrology Using Off-theShelf Tv Cameras and Lenses", IEEE Journal of Robotics and Auto mation RA-3, 4, pp.323-344, 1987.

*13:H. Saito, T. Kanade, "Shape Reconstruction in Projective Grid Space from Large Number of Images", IEEE Proc. Computer Vision and Pattern Recognition, Vol.2, pp.49-54, 1999.

*14:矢口 悟志, 木村 誠, 斎藤 英雄, 金出 武雄, "未校正多視点カメラシステムを用いた任意視点画像生成", 情報処理学会論文誌:コンビュータビジョンとイメージメディア, Vol.42, No, SIG 6 (CVIM). pp.9-21, 2001.